


Next: Performance measurements on
Up: Data-parallel molecular dynamics with
Previous: Introduction to parallel
Even if the implementation cited above is using the Connection Machine
hardware with extremely high efficiency, there is an algorithmic
problem: When forces are computed between atom pairs in neighboring
grid-cells, many of the forces are in fact computed for pairs whose
interatomic distance is greater than the cutoff-radius of the
interactions.
A kind of ``algorithmic efficiency'' can be estimated as the number of
``relevant'' non-zero interactions compared to the total number
of calculated interactions as follows: If the cutoff-radius (or rather
the radius at which the smooth cutoff-function employed in the EMT is
considered to be effectively zero) is equal to the grid-cell side
length D, the volume of the sphere of non-zero interactions around a
given atom is  , whereas the interactions are
computed inside a volume
, whereas the interactions are
computed inside a volume  for local
for local  interaction
subgrids. The ratio of these volumes, which is an estimate of the
algorithmic efficiency of the force computation, is approximately
0.155. If the code uses local
interaction
subgrids. The ratio of these volumes, which is an estimate of the
algorithmic efficiency of the force computation, is approximately
0.155. If the code uses local  subgrids and a cutoff-radius of
subgrids and a cutoff-radius of
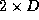 , the algorithmic efficiency is a much better 0.268. We
implemented[4] a skipping of some cells in the
, the algorithmic efficiency is a much better 0.268. We
implemented[4] a skipping of some cells in the 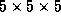 subgrid,
leading to about 20% improvement of this algorithmic efficiency.
Larger local subgrids could be used, at the cost of more communication
and a decreased number of atoms per cell. This would lead to decreased
load-balance, however, so there is an upper limit to proceeding along
this line.
subgrid,
leading to about 20% improvement of this algorithmic efficiency.
Larger local subgrids could be used, at the cost of more communication
and a decreased number of atoms per cell. This would lead to decreased
load-balance, however, so there is an upper limit to proceeding along
this line.
Thus we conclude that a fairly low upper bound to the algorithmic
efficiency of using local  subgrids exists, when
all interactions are computed. One possible resolution of this
low efficiency is to use the classical Verlet neighbor-list
method[5], but in the context of a parallel algorithm. One
implementation of such an algorithm by Tamayo is discussed in ref.
[3] (section 5).
subgrids exists, when
all interactions are computed. One possible resolution of this
low efficiency is to use the classical Verlet neighbor-list
method[5], but in the context of a parallel algorithm. One
implementation of such an algorithm by Tamayo is discussed in ref.
[3] (section 5).
We have implemented a standard Verlet neighbor-list algorithm in the
context of our previously described parallel MD algorithm[4],
with the aim of achieving the fastest possible execution time at the
expense of using large amounts of RAM memory for storing neighbor-list
related data in each parallel node.
Thus we are explicitly not aiming for simulating the largest
possible systems, but rather on the fastest solution of more
modest-sized systems (of the order of 1 million atoms). This tradeoff
was decided in view of the physics that we want to investigate.
Another aspect that influences algorithmic choices is the fact that our
EMT interactions, which are more appropriate for simulating metallic
systems, require more than 10 times the number of floating-point
operations per pair-interaction, than for the case of Lennard-Jones
interactions which are usually employed in MD studies. Hence
communications overheads in our algorithm will be intrinsically much
less significant than for the simpler Lennard-Jones interactions.
The implementation of a Verlet neighbor-list algorithm in a
data-parallel CM-Fortran MD code is relatively straightforward. The
task that distinguishes the data-parallel implementation from the usual
serial one is the access to data in non-local processors. Our choice
is to simply copy the data (atomic  coordinates, plus
some interaction data) from the nearby
coordinates, plus
some interaction data) from the nearby  local subgrid into the
memory of the local processor. The CSHIFT Fortran-90 intrinsic
is used for copying the data. This task is sketched in Fig. 1, and it
is carried out whenever the atoms are moved.
local subgrid into the
memory of the local processor. The CSHIFT Fortran-90 intrinsic
is used for copying the data. This task is sketched in Fig. 1, and it
is carried out whenever the atoms are moved.

Of course, a smaller part of the data will not represent neighbors of
any atom in the central cell of Fig. 1, and hence this data could in
principle be omitted. Also, it can be argued that it is a waste of
memory to replicate atomic data from 26 neighboring cells. This is a
deliberate choice that we have made: We want the most regular (and
hence the fastest) communication pattern of data between the
``vector-unit'' memory of the CM-5E nodes. We also want all atomic
data in a linear list in memory so that a Verlet neighbor-list
algorithm can be implemented simply and efficiently. Our aim is to get
the fastest possible execution at the cost of using extra memory.
Since the 128-node CM-5E machine at our disposal has 128 MB of memory
per node, and we want to simulate systems of only up to 1 million
atoms, we can easily afford to use memory so freely.
With all relevant data available in the local memory of each node,
there remains to construct the neighbor lists for each atom. Owing to
all the atomic data from the central and neighboring cells being arranged
in a simple linear list in local memory, it is a simple matter to
traverse the list in a data-parallel fashion for each atom in the
central cell and add any neighbors to a list of pointers (the
neighbor-list). In CM-Fortran the atom-atom distance is calculated by
a FORALL statement, and the decision whether to include the atom
in the neighbor-list is implemented by a MERGE Fortran-90 intrinsic
function. The pointers to atoms are added to the list by a ``scatter''
operation, which was first coded as a FORALL statement, but since
the present CM-Fortran compiler (version CM5 VecUnit 2.2.11) hasn't
implemented indirect memory access efficiently for 3-D arrays, we
decided to use the faster CM-Fortran library CMF_ASET_1D
routine in stead.
The performance-critical part of the above construction is the
``scatter'' operation, which requires local indirect-memory addressing
that is emulated in software on the CM-200, but which has direct
hardware support on the CM-5, so that the CM-5 can execute the
neighbor-list construction exclusively with efficient vector operations
on local memory. For the CM-200 the indirect-memory addressing was
found to be too slow for a production code, so the present algorithm
wasn't pursued any further on this hardware.
Since the CM-Fortran compiler generated sub-optimal code for local
indirect-memory addressing, the CM-Fortran neighbor-list loop (a total
of 7 Fortran statements) was translated into the CM-5 vector-unit
assembler ``CDPEAC'', taking optimal advantage of indirect-memory
addressing instructions and overlapping of computation and load/store
operations. This resulted in a speedup of the neighbor-list loop by
approximately a factor of 4. We also experimented with CM-Fortran
``array aliasing'' in order to aid the compiler's code generation, and
while improvements were seen, the CDPEAC code was still more than twice
as fast as the compiler's code.
After this optimization, an update of the neighbor-lists consumes a
time roughly equal to the time for a single MD timestep. This means
that the classical trick of increasing the cutoff-radius by adding a
skin radius must be used in order to re-use the neighbor-list
during several MD timesteps. We monitor exactly the atoms' deviations
from their positions at the time of the neighbor-list construction, and
when the maximum deviation exceeds half of the skin radius, an update
of the neighbor-list is carried out. We believe that it is important
not to postpone updates beyond this point, since the MD simulations
would then not conserve energy. Atoms will migrate between cells
during the simulation, and such migration-updates are performed prior
to the neighbor-list updates.
When atomic forces are calculated and summed in a loop over the atoms
in the neighbor-list, a simple parallel ``gather'' operation of the
neighbor-atoms' data is performed using FORALL on the data
structure sketched in Fig. 1. When the atomic data are in CM-5
vector-registers, the forces can be calculated by the EMT method as in
ref. [4]. Again, the efficiency of the force computation
depends partially on the compiler-generated code for indirect-memory
access, but less so than for the neighbor-list generation because many
floating-point operations are executed for each ``gather'' operation.
We have considered CDPEAC coding of the ``gather'' operation, but
so far this hasn't been done.



Next: Performance measurements on
Up: Data-parallel molecular dynamics with
Previous: Introduction to parallel
Ole Holm Nielsen
Thu Aug 24 15:57:03 MET DST 1995
 , whereas the interactions are
computed inside a volume
, whereas the interactions are
computed inside a volume  for local
for local  interaction
subgrids. The ratio of these volumes, which is an estimate of the
algorithmic efficiency of the force computation, is approximately
0.155. If the code uses local
interaction
subgrids. The ratio of these volumes, which is an estimate of the
algorithmic efficiency of the force computation, is approximately
0.155. If the code uses local  subgrids and a cutoff-radius of
subgrids and a cutoff-radius of
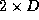 , the algorithmic efficiency is a much better 0.268. We
implemented[4] a skipping of some cells in the
, the algorithmic efficiency is a much better 0.268. We
implemented[4] a skipping of some cells in the 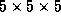 subgrid,
leading to about 20% improvement of this algorithmic efficiency.
Larger local subgrids could be used, at the cost of more communication
and a decreased number of atoms per cell. This would lead to decreased
load-balance, however, so there is an upper limit to proceeding along
this line.
subgrid,
leading to about 20% improvement of this algorithmic efficiency.
Larger local subgrids could be used, at the cost of more communication
and a decreased number of atoms per cell. This would lead to decreased
load-balance, however, so there is an upper limit to proceeding along
this line.
 subgrids exists, when
all interactions are computed. One possible resolution of this
low efficiency is to use the classical Verlet neighbor-list
method[
subgrids exists, when
all interactions are computed. One possible resolution of this
low efficiency is to use the classical Verlet neighbor-list
method[ coordinates, plus
some interaction data) from the nearby
coordinates, plus
some interaction data) from the nearby  local subgrid into the
memory of the local processor. The CSHIFT Fortran-90 intrinsic
is used for copying the data. This task is sketched in Fig. 1, and it
is carried out whenever the atoms are moved.
local subgrid into the
memory of the local processor. The CSHIFT Fortran-90 intrinsic
is used for copying the data. This task is sketched in Fig. 1, and it
is carried out whenever the atoms are moved.
